OnParsers
Written in August 2021. Minor updates in 2023.
Introduction
I hang out in a couple programming language development chat channels and new people often seem to ask the same practical questions about parsing and implementing parsers. So I wanted to write up a quick guide about the pragmatic implications of how these things work in the real world.
This assumes that you already have some idea of what a parser does and where it fits in a compiler’s pipeline, and are trying to put that theory into practice and grapple with all the choices involved. If you don’t know what a parser, lexer or abstract syntax tree are, you’ll need more background before this is useful. Come back after doing a light read of the first few chapters in one of the following books. This is also specifically for programming languages; parsing data formats uses the same general mechanics, but has different priorities.
Textbooks
I used to read a lot of textbooks about building languages and compilers, though mostly before 2010 or so. Most of them were written based on assumptions and research developed from the 1970’s to the 1990’s, when programming languages were very different beasts than they are today. Because of this they had some advice and design rules in them which is now outdated. Mainly:
- Parsing is slow. No it isn’t. Parsing was slow, in the bronze age when optimizers were simple and you didn’t have enough memory for a multi-pass compiler. For production grade compilers, the major costs are type checking and backend work. Parsing performance only matters once everything else in the pipeline can keep pace with it. Of course, you can make parsing your bottleneck if you try hard enough, especially if you want to make an incremental compiler or language server, but for most people it won’t be a problem for a while.
- Everyone uses parser generators. No they don’t. Parser generators are great force amplifiers when used well, but also are not always the easiest things to use well. They are general-purpose tools, and occasionally people end up writing special-purpose tools to replace them. There’s nothing wrong with hand-writing a parser, one way or another.
The most actually useful books I’ve read:
- Crafting Interpreters by Robert Nystrom. Interpreters and compilers are pretty close in many respects, and for frontend are essentially identical. This book is great in general.
- Modern Compiler Implementation In C/Java/ML by Andrew Appel. Kinda out of date now, but top tier for the era it covers.
- Compilers: Principles, Techniques, and Tools by Alfred V. Aho, Monica S. Lam, Ravi Sethi, and Jeffrey D. Ullman. AKA The Dragon Book, which may be the best name for a book ever. The canonical textbook for university compiler classes, and one of those textbooks you want to keep after the class. The main disadvantage is it’s kinda written as a reference book, not a tutorial leading you through the whole process of building a compiler. Apparently there’s a second edition as of 2006, I should read it.
Online sources:
- https://blog.jeffsmits.net/compsci/2024/04/07/parsing-and-all-that/
- https://courses.cs.cornell.edu/cs4120/2022sp/notes/
Lexers
Lexers seem to be basically a solved technology. I said that “everyone uses parser generators” is false; “everyone uses lexer generators” is a little bit more true. A lexer just turns a stream of characters into a stream of tokens; it’s not that complicated, and there’s only so many good ways to do it. There’s details like push vs. pull lexers, normal vs. extended regexes, and so on; the details are interesting, but not super important if you’re just getting started. If you want to hand-write a lexer for fun or to learn how it works, go ahead, but don’t feel obligated to.
You can integrate lexing and parsing together into one step, and this seems to be the preferred way of using parser combinators (see below), but the practical gains to it seem to be minimal in most cases. One place it does seem to be commonly used is when making tools that are designed to manipulate multiple different languages, such as IDE’s or other code manipulation tools. For implementing a single programming language, this is not very important. Usually lexing is there because it makes things easier
The Theory
Back in the 50’s and early 60’s when things we would recognize as high level languages were first being created, nobody really knew what a good high level programming language looked like, let alone how to make one that was particularly useful for humans to read and write. What constructs did humans need or not need? Which ones did they like or not like? Plus, nobody really knew how to make computers read complex human-like text anyway, and a lot of research was being done on that. This also coincidentally lined up with research also being done at the time in human linguistics which seemed very exciting and world-changing. (It didn’t change the world, but did maybe change how we think about the world a bit.) And so people making programming languages were very concerned about the theoretical foundations of the shape of the language and how it was parsed.
Those days are over; there’s interesting and useful theoretical stuff
to be discovered and created, but in practical terms we have a pretty
useful toolbox of parsing methods that doesn’t need a lot more research
to be done to it, at least until the next big breakthrough. To compare
different sorts of parsing problems we use the concept of the “power” of
a parser or language description. Essentially, if you can write a parser
using algorithm A, and another using algorithm
B which can parse everything A can plus a few
things that A cannot, then algorithm B is more
“powerful” than algorithm A. In the broad strokes of the Chomsky
Hierarchy we have several nicely-nesting classes of grammar/parser
that describe the sort of state machine you need to parse it, from least
to most powerful:
- Regular languages. These are good at recognizing simple patterns but can’t do much of anything in the way of recursion, self-reference, etc. The most common regular language is regular expressions, though regexp’s are usually extended in somewhat ad-hoc ways to be more powerful than just a regular language. The classical example of the limitations of regular languages is that you can use a regular expression to try to slurp in a parenthesis-delimited pattern, but it can’t ensure that the parens are correctly balanced without outside help. You can parse/match/recognize/evaluate any regular language using a state machine with a fixed amount of memory.
- Context-free languages. If a language/grammar is “context free” this means that in any state you can look at a fixed-sized chunk of the input and always figure out what state to switch to next. These are what we use for programming languages ’cause they’re powerful enough to parse complex structures, but it’s still relatively easy to make parsers and grammars for a reasonable subset of them. They’re a sweet spot in the balance of simplicity vs. flexibility. You can parse any context-free language using a state machine with only a stack for dynamic memory.
- Context-sensitive languages. I believe the difference from context-free languages is that a rule may have to look at arbitrary parts of the input to figure out what rule to switch to next. Sometimes these are used for natural language processing – they’re still not actually good at understanding natural language from what I’ve seen, just describing it. Sometimes a grammar that is ambiguous in a context-free language can be parsed by a context-sensitive parser, but in practical terms these ambiguities are usually treated as minor special cases. Avoid them where you can, and in the places you can’t just extend your context-free parser a little to handle the special case as a one-off. You may need unbounded amounts of memory to parse context-sensitive languages.
- Unrestricted languages. ie, everything else. Parsing an unrestricted language is equivalent to running a Turing machine, with the halting problem and all the fun that sort of things that causes. Probably not what you want; having a parser that does not terminate is generally regarded as impolite to your users.
This hierarchy matters, but a bit less than you might think since in practice the boundaries are fuzzy. The main take-away of this is that if you try use a regular language for your programming language you’re likely to end up hacking around its limitations, and if you end up needing something much more powerful than a context-free language you’re setting yourself up for a tough time. However, there are real languages such as C that need minor hacks to be parsed by a context-free algorithm, so you can do it within limits. But my feeling is always that if you have a language that is very difficult for a computer to parse, the humans reading and writing it aren’t going to have a terribly fun time either.
One question I’ve seen a few times is, do you need to write down a full precise grammar for your language? Do you need to know EBNF like the back of your hand? The answer to both is… no, not really, but in my experience it will be very useful up to a point. A grammar is a blueprint of your language, and EBNF is the lingua franca notation to use for it. (Also like the French language, there’s a million little dialects of EBNF with varying levels of mutual intelligibility; choose one that works for you.) How detailed you want your grammar to be depends on how detailed it needs to be for your purposes. People like Niklaus Wirth who are held up as exemplars of syntax design also tend to give the impression that a perfect grammar springs, like Athena, full-formed from their mind. Very few things actually do that in the real world. You don’t have to agonize over the perfect grammar before you start making your language. You’re going to tweak and fiddle and refine it bit by bit as your language grows and evolves.
The Practice
When parsing context-free languages there’s a lot of terminology and
subcategories, starting from the basic division of “top-down parsers”
vs. “bottom-up parsers” and getting more woolly from there. Some of
these parsers are more powerful than others, and none of the ones
described here can parse all context-free grammars (which is
somewhere between O(n^2) and O(n^3) in time
complexity). Instead they parse useful subsets of context-free grammars
particularly easily, generally in O(n) time or close to it.
They’re all roughly similar in power, but the overlapping
relationships between them are complicated and ambiguous enough that
it’s probably not worth worrying about too much. Any of them can be and
have been used to make a decent programming language syntax. However,
they result in very different sorts of code for your parser, so we’re
going to go through the major tools in your toolbox:
- Table-driven parsers
- Recursive descent parsers
- Parser combinators
- Parsing expression grammars (PEG’s)
Table driven parsers
Table driven parsers are all based on having a state machine represented by a table describing what transitions are allowed between states. A small piece of the input token stream is used as a lookup index into the table to tell you what the next rule in your state machine is, and you just read tokens and check against the table in a loop. They are fast, efficient, pretty easy to construct by hand (if somewhat tedious), and it’s very easy to make a parser generator spit one out. In practice, you’re usually going to encounter these as the output of parser generators. Table driven parsers are also a gigantic pain in the butt to debug and alter; my experience is you either spend a lot of time with a paper and pencil agonizing about what ambiguity you’ve missed, or stare at a giant pile of parser generator errors doing the same.
The first major type of table driven parsers are LL(k),
“Left-to-right, leftmost derivation, with k tokens of lookahead”. Common
values of k are 0 or 1, but you can make just about
anything work fine as long as there’s a fixed upper bound to it. Nobody
seems to outright say it, but if your value for k is more
than 2 you’re probably making life complicated for yourself somehow.
These are top-down parsers, where you read tokens into a
list/queue/stream/whatever, and your state machine looks at (up to) the
first k tokens trying to match a rule. If it matches, it
removes those tokens from the front of the list and switches to the
matching state. If it doesn’t match, you either have a parse error, or
you keep reading more tokens up to your maximum k. There
are also parser generators out there that implement an LL(*) algorithm,
ie they just try to look ahead as far as necessary for a particular
rule, somewhat similar to recursive descent parsers.
After that you have LR(k) parsers, “Left-to-right, rightmost
derivation, with k tokens of lookahead”. Again common values of
k are 0 or 1 but can be anything. These are the bottom-up
complement to LL(k) parsers: they read tokens onto a
stack, then the state machine looks at the
last k tokens of the stack trying to match
a rule. These are a bit more powerful than LL(k) grammars; any LR(k)
grammar is more powerful than a LL(k) grammar. But there’s no guarantee
that it’s more powerful than an LL(k+1) grammar, so in practice the
difference isn’t terribly important.
LR grammars are more popular in parser generators than LL because there are good algorithms known for quickly generating fast parsers from a description of rules, often generating a particular variant or implementation of full LR(k) parsing such as SLR, LALR, GLR, shift-reduce parsers, and so on. However, anecdote says that LR parsers are harder to generate good error messages for than LL parsers, because the part of the token stream the state machine is looking at when it notices the error doesn’t necessarily contain the token that is the root cause of the error. My personal experience is that parser generators in general are more painful to use than hand-writing a parser as long as you have a good idea of what you want your language to look like, though if you know how to use one well they can make your life far easier.
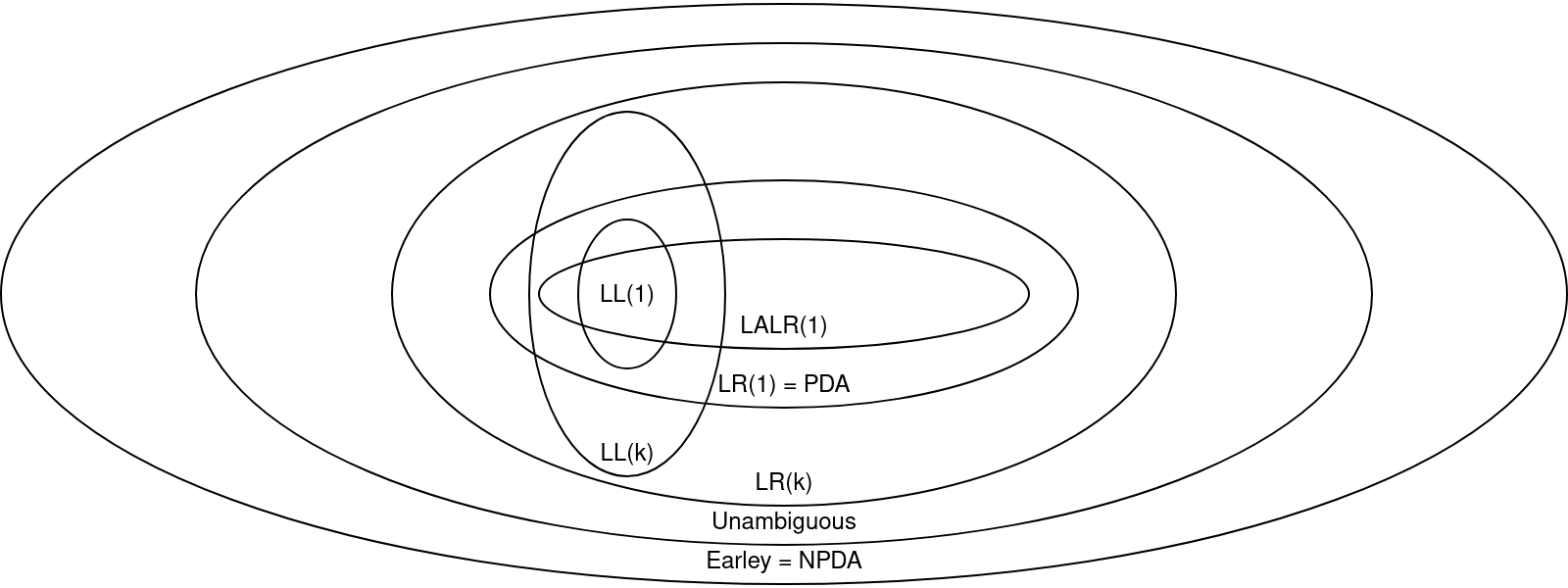
Here, have a diagram (from https://courses.cs.cornell.edu/cs4120/2022sp/notes/):
Recursive descent parsers
I’ve fallen in love with recursive descent parsers a little since I
wrote my first really nontrivial one. These are top-down parsers that
are again written as state machines, but instead of a look-up table of
states you have a bunch of functions that check what the next
k tokens are in the input stream and call each other
recursively. One function per state/rule, and the transitions between
states are represented by the function calls. They are easy to write,
fairly easy to read, and generally quite nice to work with. They are
about equivalent to LL(k) grammars in power, so they’re not the
most general things in the world, though you also can code
whatever special cases you feel like into any particular rule that needs
it. A table-driven parser can be faster, but generally not
enough to be a huge deal. If recursive descent parsers have a downside
it’s that they are a little verbose and refactoring them can be tricky,
since if you drastically change the structure of your grammar you’ll
have to go and rewrite/rearrange all the functions involved. However,
extending them with new rules or changing the structure of a
few rules without needing to touch other parts of the grammar is quite
simple.
The best way I’ve found to write a recursive descent parser is to start with a vaguely complete EBNF grammar written down somewhere, then go through it rule by rule and write a single function implementing each rule from the terminals to the root. You can note which rule each function implements in a comment to make it convenient to look back at later, and all in all I’ve found it very easy to look at a rule and a function and verify that they do the Right Thing. You can also unit test each function more or less in isolation of the others, working from the terminal leaves of your grammar up to the root. Also, because you are writing all these functions by hand instead of using some sort of generator, they can have whatever signature or framework you want around them, so stuff you want to do as you parse such as collecting context for error messages or interning symbols doesn’t need to work around an existing API.
There are also recursive ascent parsers, which are the complement to recursive descent: a state machine implemented as function calls, but which build their parse tree bottom-up. I’d never heard of them before a few weeks ago, but they sound cool, and anecdotally have similar advantages.
Parser combinators
These are a relatively new kid on the block. All the aforementioned
stuff was developed in the 1960’s and 70’s, while parser combinators
seem to have been developed in the 90’s and popularized in the 2000’s by
some Haskell libraries. Parser combinators are a method of implementing
recursive descent parsers by composing higher-order functions, rather
than writing procedural code that manipulates a state machine with if’s
and loops. Thus your parser ends up feeling a little bit more like
composing patterns in a regular expression, while being as powerful as
any recursive descent parser.
if next_token == Foo || next_token == Bar { parse_foobar() }
becomes something like either(Foo, Bar).then(parse_foobar).
They can be very concise and flexible if you can wrap your brain around
them well.
People kinda seem to love these or hate them, as far as I can tell. Personally I’ve never had great success with them for complicated cases but have found they can be very nice for simpler cases such as parsing binary file formats. They are especially nice in functional languages that dislike mutable state, and can run very fast if the implementation is good. Like recursive descent parsers, if you write your grammar well you can make it line up very nicely with the functions you actually define with your parser combinators, and the extra conciseness can make refactoring and modification simpler when things change.
Parsing expression grammars – aka PEG’s
These are also a relatively new technique, discovered in 2004. Parsing expression grammars are technically a slightly different way of looking at the world than context-free languages, but are equivalent enough in power to parse a programming language. They are able to be used in parser generators to generate efficient parsers using an algorithm called “packrat parsing”, while being similar to top-down parsers in most other respects.
One nice property of PEG’s is that they are never ambiguous. The
parser will never say “I could choose one of these two rules and I don’t
know which one to choose”, it always has one rule it prefers over the
other. The downside of this is that the rule that it chooses isn’t
necessarily the one you want it to unless you tell it which it
should prefer, and it won’t necessarily warn you that decision needs to
be made. In this way they are similar to recursive descent parsers,
which can always resolve ambiguities just by having the preferred rule
come first in a chain of if’s. The ambiguity still exists,
it’s just up to you how to special-case it, and if too many ambiguities
build up your language will end up a mess of little besides
special cases. Still, this is an appealing property when you’re sick of
a parser generator spitting out 302 reduce/reduce conflicts after a
trivial-looking change, and PEG’s seem to work well in practice.
One anecdotal down-side of PEG’s is that, similar to LR parsers, it can be difficult to get good error information out of them. If you have a sequence of patterns that are tried in order, as described above, and the programmer is trying to write the pattern described by the first patterns and makes a syntax error, then the parser will still go through all the patterns before giving up and saying “this can’t be right”. If it tries two, or three, or four patterns in sequence and none of them match, it has no way of knowing that the first pattern was what was actually intended. There are apparently pragmatic ways around this, but it’s still problematic.
Expression parsing
Most programming languages have a syntax designed to make life easy for their parsers. The language designer can insert delimiters or operators to make it easy to figure out what’s going on from only reading a few tokens, expressions or statements can be structured so that certain terms can only appear in certain places, you can even use sigils for different types or scopes or such so the programmer has to be more specific about what is going on. You can be simple and workmanlike with a bunch of keywords delimiting simple statements like Lua, or you can make a relatively few syntax constructs do a lot of interesting work like Haskell. Generally there will be some way or another you can make a nice, unambiguous syntax within the limited power of your parsing algorithm.
All this falls down with our humble conventional infix mathematical
notation, b = a*x+y. There’s two problems: You have lots of
recursive constructs which are intermixed with each other, and how they
are intermixed depends on precedence rules for infix tokens between the
recursive components. Basically, a top-down parser will generally read
from left to right, a bottom-up parser will read right to left, but
neither of those fully encompasses our common math notation in
a simple way. It’s one of those things that isn’t really a
problem, but it is totally a pain in the ass. The year
in fourth grade memorizing “Please Excuse My Dear Aunt Sally” for
“parenthesis, exponents, multiply/divide, add/subtract” becomes the bane
of your existence unless you approach it with a bit of savvy. Adding
prefix and postfix operators to the infix-operator mess only makes life
more difficult. Then we like to add more infix operators like
== and > with their own precedence rules
just because life wasn’t hard enough!
Of course, it’s your language, you can simply change the rules to
make it easy. If you treat math operations like any other function, the
way Lisp or Forth does, operator precedence becomes a non-issue. I
actually like that approach a lot, and rather want to make a language
someday that casually forces you to write all your math in Forth-like
RPN. Or you can also make the problem go away by treating math
operations as having no precedence, so a * x + y is always
(a * x) + y and a + x * y is always
(a + x) * y (or group to the right instead), though you
might have a Fun time making it jibe with other infix operators the way
you want to. I’ve seen some people advocating that and honestly think it
would probably work pretty well, though it would also take some getting
used to. But if you go this sort of route be aware you’re spending some
of your Strangeness
Budget on it.
The essential problem is that you will want to write a rule that
looks something like
expression ::= expression OPERATOR expression, and having
that recursive rule on both sides of the operator will make your parser
explode. So you need a way to make it not do that. There are known
techniques to rewrite the inconvenient part of your grammar to
remove that recursion, implementing operator precedence via a chain or
loop of grammar rules. But, I can never remember how to do it and have
trouble doing successfully; it’s an approach my brain just slides off
of. Plus, if you want to change the precedence of some of your operators
and they’re encoded in the structure of your grammar you have to figure
out how to re-do it all over again. Maybe your brain is wired
differently than mine and can handle the transformation, give it a try.
But for me doing it that way generally results in my grammar becoming an
incomprehensible goop, either immediately or later when I come back to
try to change something and have to re-understand what it’s doing.
People also argue that rewriting the grammar this way results in a
slower parser, but as usual, I don’t care about that until a profiler
tells me it’s a bottleneck. The rewriting process itself is what gets
me.
Because of this people often find it more useful to use a
special-case algorithm for parsing these sorts of math expressions.
There are several types: “Pratt parsing”, the “Shunting-yard algorithm”,
“precedence climbing”, “operator-precedence parsers”, and probably more
that I don’t know about. They’re all somewhat related, and some of them
such as Pratt and shunting-yard are basically different algorithms for
the same process. Pratt
parsing
is my personal favorite, at least partially ‘cause it involves a while
loop with a recursive call in it, which is a great workout for the ol’
grey matter. But whichever technique you choose they all achieve the
same result: you write a mini-parser that is good at infix operators but
maybe not what you want to use for the rest of your language, and slot
it into your parse_expression() to make life simpler. I
highly recommend checking them out.
Designing your syntax
Syntax “doesn’t matter”. It really doesn’t matter, because people will adapt to anything and become good at using it, if they have a good reason to. No matter what, the actual writing of characters in source file is the easy part of programming, and the hard part all happens in your head. However, syntax is also the user interface to the tool you are creating, and so it is the part where rough edges are most obvious. This is why syntax gets a disproportionate amount of attention and argumentation: it’s the first thing people encounter, and people dislike needing to rewire their muscle memory to deal with a new syntax. It’s like the handle of a hammer or drill that a carpenter uses every day: it’s not going to dramatically change how the hammer hits or the drill drills, but you want to make something that feels comfortable in the hand, even though everyone’s hand is a little different.
Unfortunately researching what syntax works well is hard, because there’s not a whole lot of money in it and any experiment involving humans’ brains and perceptions is going to be a lot of work. So we don’t have a great deal of unambiguous, replicated science telling us what kind of syntax things are good or bad, but instead have 70+ years of anecdote, rumor, best practices, mistakes, and lots and lots of ever-shifting fashion. However we do have some long-standing traditions for designing syntax, empirical patterns that have stood a few decades of fashion and evolution. I’ve tried to pick a few general guidelines out of that; these will probably mutate or refine with age, but we can more or less say that for now:
- No matter what you do, someone will hate it.
- Any syntax is equally foreign to new programmers, or close enough.
- Experienced programmers generally like syntax that looks kinda like syntax they already know.
- Trying to make syntax similar to human language will generally be misleading, since it will have limitations that human languages don’t.
- Try to avoid things that look similar to each other or are easily mistaken for each other; ambiguity is always evil. (Though it’s sometimes also very convenient.)
- Keeping things concise is nice, but keeping things easily accessible to modern programming tools like linters or auto completion will get you further in the long run. (Debatable, but this is where I see current trends going.)
Of course, if you want to break the bonds of convention entirely, go right ahead. But if you just want to make something that works reasonably nicely, the easy way to do this is to steal some other language’s syntax and use it as a starting point for your own. I personally identify a few broad categories of syntax “styles” in popular languages: C-like (C, Java, D, etc), Lisp-like (Common Lisp, Scheme, Clojure), and Haskell-like (Haskell, OCaml, F#, etc). Then there’s smaller related families like Pascal-like (C-like but with more keywords and fewer sigils), hybrids such as Rust (Haskell-like dressed up in C-like clothing) or Erlang (something between Haskell-like and Prolog) and Forth (which is like very little else in the world). Plus there’s plenty more (major!) categories I haven’t mentioned. They all work though, so starting from one of these broad styles you like is often useful.
But in the end, it’s the least important part of the language, and one of the easier (if annoying) parts to change. Choose one you like, or make up your own.
Often what I do these days is to deal with syntax second: I write my language’s abstract syntax tree first, possibly carrying on into making the compiler backend. Once I like the AST, I write a parser for it, then carry on from there adding features and changing things and such. I often have some idea of what I want my syntax to look like, but that often needs to change a bit to accommodate the realities of my AST. You don’t need to start your compiler by deciding on a syntax and writing a parser. However, having a parser is very useful because it makes it easy to write tests, refer to parts of it in notes, and play with your language to explore parts that are incomplete or undecided. So don’t put it off too long.
Just remember, the syntax is the user interface of your language. To quote the most genre-savvy patch note I’ve ever seen, no matter what you choose “some of you will love it, some will hate it. You’re welcome and we’re sorry.”
Investigation
Here’s some research into what parsers for real compilers and interpreters do. Note this is not necessarily 100% accurate, since some of these compilers are quite complicated and either I may mistake one thing for another, or the parser might get altered or rewritten. I believe they are correct as of the writing of this article.
- clang – Recursive descent parser with something that looks like an operator-precedence expression parser
- clojure – Recursive descent parser (naturally; they are a proverbially good fit for Lisp syntax)
- CPython – PEG grammar with home-made parser generator
- D – Recursive descent parser of some kind I think
- Erlang and Elixir – Uses the yecc parser generator (LALR)
- gcc – Recursive descent parser with operator-precedence expression parser
- ghc – Uses the Happy parser generator (LALR)
- go – Recursive descent parser with Pratt(?) expression parser
- javac – Recursive descent parser with operator-precedence expression parser
- Lua – Recursive descent parser(?) with Pratt expression parser
- nim – Recursive descent parser, no separate expression parser
- OCaml – Uses the menhir parser generator (LR(1))
- Ruby – Uses the yacc/bison parser generator (LALR)
- rustc – Recursive descent parser with precedence climbing expression parser
- zig – Recursive descent parser, no separate expression parser
…this was a lot less diverse than I expected, to be honest. But hey, use what works.
Discussion
Comments on lobste.rs include some interesting discussion on this article, and corrections which have been incorporated.
Excellent guide on actually implementing parsers here, though it leaves out pratt/operator-precedence/precedence climbing which I feel makes life harder than it has to be: https://tratt.net/laurie/blog/2020/which_parsing_approach.html . I actually disagree with like 80% of his conclusions but he does a good job of covering his bases.
Other nice resources: * https://www.abubalay.com/blog/2021/12/31/lr-control-flow